Promover o ensino precoce das operações numéricas nas creches e pré-escolas

Introdução

Há muito tempo, a melhor maneira de ajudar os alunos a aprender as operações de adição básica com um dígito, como 3+4=7 e 9+5=14, e as operações de subtração relacionadas, como 7–3=4 e 14–9=5, já é objeto de debates (ver, por exemplo, Baroody & Dowker,¹ especialmente os capítulos 2, 3, 6 e 7). Entretanto, existe uma concordância geral de que as crianças devem conseguir dominar as operações.² O domínio das operações implica saber fazer somas e diferenças de forma eficaz (com rapidez e precisão) e aplicar esses conhecimentos de forma apropriada e flexível. Ao longo das quatro últimas décadas, ficou cada vez mais claro que os conhecimentos matemáticos do dia-dia (informais) das crianças constituem uma base importante para o aprendizado da matemática na escola (formal).^3,4,5 Por exemplo, as pesquisas indicam que o fato de ajudar as crianças a desenvolver sua percepção dos números pode promover o domínio das operações.^6,7,8,9 O objetivo do presente artigo é o de resumir como o desenvolvimento de uma percepção informal dos números antes de completar o primeiro ano do ensino fundamental fornece as bases da habilidade chave formal de dominar as operações nos primeiros anos de escola primária.

Questões-chave de pesquisa

1. Em que momento os pais e educadores da primeira infância devem iniciar: (a) o processo de promoção da percepção dos números, e (b) os esforços para estimular diretamente o domínio das operações?
2. Quais são os pré-requisitos desenvolvimentais que as crianças das creches e das pré-escolas devem aprender para conseguir dominar as operações de forma eficaz?
3. Qual é o papel da linguagem no desenvolvimento desses conhecimentos fundamentais?
4. Como os pais e educadores da primeira infância podem incentivar da forma mais eficiente possível a percepção dos números e o domínio das operações? 

Resultados de pesquisas recentes

Pergunta 1. O processo de ajudar as crianças a desenvolver sua percepção dos números – a base do domínio das operações – pode e deve começar durante os anos pré-escolares. Pesquisas recentes indicam que as crianças começam muito cedo a desenvolver sua percepção dos números. De fato, alguns bebês de apenas 18 meses e quase todas as crianças de 2 anos de idade já começaram a aprender os pré-requisitos desenvolvimentais para o domínio das operações (por exemplo, ver Baroody, Lai, & Mix,³ para uma análise).

O sucesso dos esforços para estimular o domínio das operações depende de duas coisas: assegurar-se de que a criança está pronta no plano do desenvolvimento e não apressá-la. Uma vez que as pesquisas indicam que diferenças individuais importantes quanto à percepção dos números já aparecem a partir dos dois ou três anos de idade e, muitas vezes, aumentam com a idade,^3,10 não existe nenhuma regra fixa e definitiva a respeito do momento de iniciar um treinamento formal relativo ao domínio das operações. Contudo, para muitas crianças, pode acontecer que, mesmo com as somas mais simples (n+0 e n+1), essa formação não seja apropriada ao desenvolvimento antes do final da pré-escola ou do início do primeiro ano do ensino fundamental.¹¹ Para as crianças que correm o risco de insucesso escolar, acontece muitas vezes que mesmo as somas mais simples não façam sentido antes do primeiro ou do segundo ano do ensino fundamental.¹² 

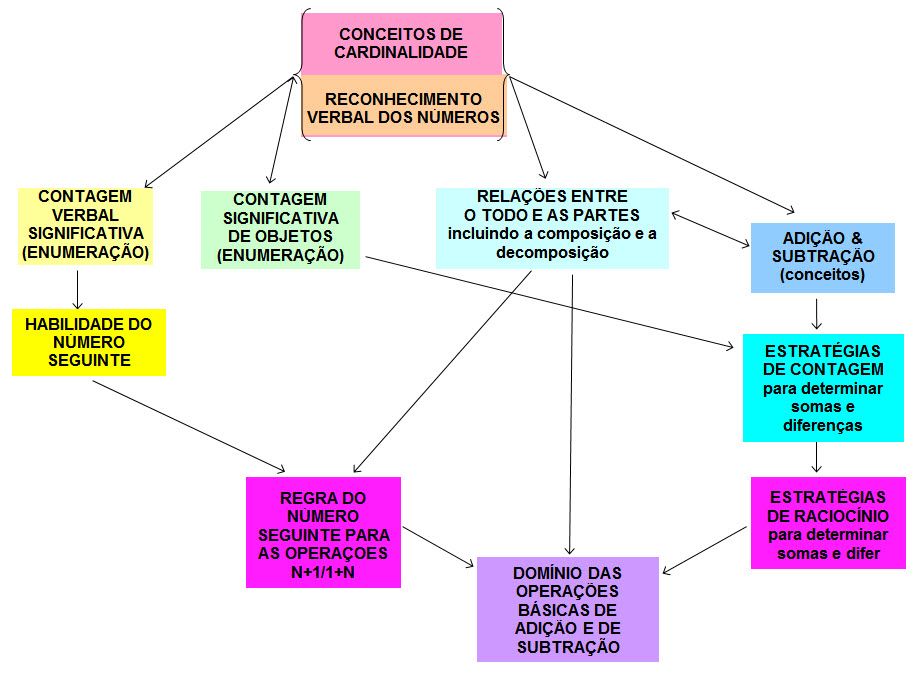
Perguntas 2 e 3. Alguns estudos indicam que a linguagem, na forma dos nomes dos primeiros números, desempenha um papel chave no desenvolvimento da percepção dos números (para uma discussão detalhada, ver Baroody;³ Mix, Sandhofer, & Baroody¹³). Mais especificamente, ela pode fornecer uma base para dois fundamentos da percepção precoce dos números, a saber o conceito de número cardinal (o número total de objetos em um conjunto) e a habilidade de reconhecimento verbal dos números (RVN), às vezes chamado de “subitizing (verbal)”, indicados no alto da figura 1. O reconhecimento verbal dos números consiste em reconhecer de forma segura e eficaz o número de objetos em pequenos conjuntos e dar-lhe o nome correto. A utilização de “um”, “dois”, “três”, junto com a visualização de exemplos e de contraexemplos de cada um pode ajudar as crianças de 2 e 3 anos a desenvolver um conceito cada vez mais seguro e exato dos “números intuitivos” um, dois e três, isto é, uma compreensão do conceito de um, de dois e de três. 

• Por exemplo, ao ver ••, DD, e  o o  (exemplos de pares), todos chamados de “dois”, as crianças pequenas podem perceber que a aparência dos objetos nos conjuntos não é importante (a forma e a cor são irrelevantes para o número). Isso pode lhes dar também um rótulo (“dois”) para seu conceito intuitivo de pluralidade (mais que um objeto). 
• O fato de ver  •, •••, D, DDD, , e    (contraexemplos de pares) chamados de “não dois” ou com o nome de outro número, pode ajudá-las a definir os limites do conceito de dois. 

As implicações-chave para o ensino são que a compreensão básica dos números cardinais não é inata e que ela não se desenvolve automaticamente (cf. Dehaene¹⁵).^14,16 Os pais e os educadores na pré-escola são importantes para fornecer as experiências e o feedback necessários para desenvolver os conceitos numéricos. Eles devem tirar proveito de situações diárias cheias de significado para denominar (e estimular as crianças a denominar) pequenos conjuntos (por exemplo, “Quantos pés você tem?” “Portanto, você precisa de dois sapatos e não apenas um.” “Você pode pegar um biscoitinho, mas não dois.”) Algumas crianças entram na pré-escola sem saber reconhecer todos os números intuitivos. Crianças assim apresentam um sério risco de fracasso escolar e precisam de um trabalho intensivo de recuperação. O serviço de detecção na pré-escola deve verificar se as crianças conseguem reconhecer imediatamente conjuntos formados de um a três objetos e são capazes de distingui-los de conjuntos um pouco maiores de quatro ou cinco objetos.

Como ilustrado na figura 1, a evolução conjunta dos conceitos cardinais dos números intuitivos e a habilidade do RVN podem fornecer as bases para uma variedade de conceitos e habilidades sobre os números, a contagem e a aritmética. Essas competências podem servir de base para uma contagem verbal significativa. A percepção dos números intuitivos pode ajudar as crianças a literalmente ver que um conjunto chamado de “dois” possui mais objetos que um conjunto chamado de “um”, e que um conjunto chamado de “três” tem mais objetos que um conjunto chamado de “dois”. Por sua vez, essa compreensão ordinal básica dos números pode ajudar as crianças a compreender que a ordem dos nomes dos números é importante quando contamos (o principio de ordem estável) e que a sequência dos nomes dos números (“um, dois, três...”) representa conjuntos cada vez maiores. À medida que a criança se familiariza com a sequência da contagem, ela desenvolve a capacidade de começar de qualquer ponto na sequência e de dizer (de forma segura) o nome do número seguinte na sequência (habilidade do número seguinte) no lugar de contar a partir de “um”.

A capacidade de citar automaticamente o número que segue imediatamente outro número na sequência de contagem pode ser a base para perceber que o fato de acrescentar “um” a um número resulta num número maior e mais especificamente, na regra do número seguinte para as operações n+1/1+n. Quando se adiciona “um”, a soma representa o número que segue o outro número na sequência de contagem (por exemplo, a soma de 7+1 corresponde ao número que segue “sete” na contagem, isto é, “oito”). Essa estratégia de raciocínio pode permitir que as crianças deduzam de forma eficaz a soma de qualquer combinação semelhante para a qual conhecem a sequência de contagem, até mesmo aquelas ainda não praticadas anteriormente como as operações de adição de grandes números com vários dígitos como 28+1, 128+1 ou 1.000.128+1. Com o tempo, essa estratégia de raciocínio se torna automática – ela pode ser aplicada eficazmente, sem necessidade de reflexão (isto é, ela se torna um elemento da rede de recuperação na memória). Em outras palavras, ela se torna o fundamento para o domínio das operações para as combinações n+1/1+n.

O RVN e o conceito de cardinalidade que ele representa podem constituir uma base para a contagem significativa de objetos.¹⁷ As crianças que conseguem reconhecer “um”, “dois” e “três” são mais suscetíveis de se beneficiar dos esforços dos adultos para mostrar e ensinar a contagem de objetos do que aquelas que não conseguem. Elas são também mais suscetíveis de reconhecer o objetivo da contagem de objetos (como sendo outra maneira de determinar o total de um conjunto) e a justificação dos procedimentos de contagem de objetos (por exemplo, que o motivo pelo qual algumas pessoas enfatizam ou repetem o nome do último número utilizado no processo de contagem é que ele representa o total do conjunto). A contagem significativa de objetos é necessária para a invenção de estratégias de contagem (com objetos ou nomes dos números), para determinar somas e diferenças. À medida que essas estratégias se tornam eficazes, a atenção fica liberada para descobrir padrões e relações; essas regularidades matemáticas, por sua vez, podem servir de base para estratégias de raciocínio (isto é, recorrer a relações e operações conhecidas para deduzir a resposta a uma combinação desconhecida). À medida que essas estratégias se tornam automáticas, elas podem servir como estratégias de recuperação na memória que possibilitarão produzir respostas de forma eficaz a partir de uma rede da memória ou de recuperação na memória.

O RVN pode fazer com que a criança veja um mais um como dois, um mais um mais um como três, ou dois mais um como três, e o contrário (isto é, três como um mais um mais um ou dois mais um). A criança desenvolve assim uma compreensão da composição e da decomposição (um todo pode ser construído a partir de elementos individuais ou decomposto em elementos individuais, muitas vezes de diferentes maneiras). O fato de ver repetidamente a composição e a decomposição de dois e de três pode levar ao domínio das operações mais simples de adição e de subtração (isto é, “um mais um é igual a dois”, “dois mais um é igual a três”, e “dois menos um é igual a um”). A decomposição repetida de quatro e de cinco, com comentários (isto é, denominando um conjunto de quatro como sendo “dois mais dois”, e ouvindo outra pessoa confirmar que “sim, dois mais dois é igual a quatro”), pode levar a um domínio das operações com as somas mais simples até cinco, e constitui uma das maneiras de descobrir a regra do número seguinte para as combinações n+1/1+n (discutida acima).

Juntos, o conceito de cardinalidade, o RVN e os conceitos de composição e de decomposição podem fornecer os fundamentos da construção de um conceito básico de adição e de subtração. Por exemplo, ao adicionar um objeto a um conjunto de dois objetos, uma criança pode literalmente ver que o conjunto de origem foi transformado em um conjunto maior de três objetos. Essas competências podem também servir de base para desenvolver uma compreensão relativamente concreta, e até relativamente abstrata, dos seguintes conceitos aritméticos¹⁸: 

• Conceito de negação subtrativa. Por exemplo, quando as crianças identificam que se você tem dois blocos e tira os dois blocos, não sobra nenhum bloco, elas podem deduzir que qualquer número tirado dele mesmo não deixa nada. 
• Conceito de identidade aditiva e subtrativa. Por exemplo, quando as crianças reconhecem que, quando se tem dois blocos e não se tira nenhum, sobram dois blocos, elas podem deduzir a regularidade segundo a qual quando não se tira nada de um número, ele permanece inalterado. Os conceitos de negação subtrativa e de identidade subtrativa podem fornecer as bases para o domínio das operações com as famílias de fatos de subtração n – n = 0 e n – 0 = n respectivamente.

Em consequência, uma baixa percepção dos números pode prejudicar o desenvolvimento do domínio das operações e outros aspectos do desempenho em matemática. Por exemplo, Mazzocco e Thompson¹⁹ descobriram que o desempenho de crianças em idade pré-escolar relativo aos quatro elementos seguintes do Test of Early Mathematics Ability – segunda edição (TEMA-2) – permitia prever as crianças que teriam dificuldades em matemática no segundo e no terceiro ano do ensino de primeiro grau: a contagem significativa de objetos (identificar que o último nome de número utilizado no processo de contagem indica o total), a cardinalidade, a comparação de números de um dígito (isto é, “Qual é maior: quatro ou cinco?”), somar mentalmente números de um dígito, e ler números de um dígito. Convém observar que o reconhecimento verbal dos números intuitivos constitui um fundamento das três primeiras habilidades e um aprendizado significativo da quarta. 

Pergunta 4. A base para ajudar os alunos a desenvolver a percepção dos números em geral e o domínio das operações em particular é de criar oportunidades para lhes permitir descobrir padrões e relações. Por exemplo, uma criança que aprendeu as “duplas”, tais como 5+5=10 e 6+6=12, de uma forma significativa (isto é, a criança identifica que todas as somas dessa família são números pares ou múltiplos de dois), pode utilizar esse conhecimento para deduzir as somas de operações desconhecidas de duplas-mais-um como 5+6 ou 7+6. 

Para serem apropriadas do ponto de vista desenvolvimental, essas oportunidades de aprendizado devem ter um objetivo, fazer sentido e ser baseadas em perguntas.²⁰ 

• As instruções devem ter um objetivo e ser atraentes para as crianças. Isso pode ser conseguido integrando instruções em brincadeiras estruturadas (por exemplo, uma brincadeira que envolve o lançamento de um dado pode ajudar as crianças a identificar padrões regulares de um a seis). As aulas de música e de arte podem servir de veículos naturais para uma reflexão sobre padrões, números e formas (por exemplo, manter um ritmo de duas ou três batidas, desenhar grupos de balões). Os pais e professores podem tirar proveito de muitas situações do dia-dia (por exemplo, “Quantos pés você tem? ... Então, quantas meias você precisa tirar da gaveta?”). As perguntas das crianças podem ser uma fonte importante de instruções cheias de significado.
• As instruções devem fazer sentido para as crianças e desenvolver pouco a pouco (e ter relação com) aquilo que elas já conhecem. Um objetivo significativo para os adultos que trabalham com crianças de dois anos é fazer com que as crianças identifiquem “dois”. Forçá-las muito rápido a identificar números maiores como quatro pode ser forte demais e fazer com que elas fiquem desestimuladas (elas ficam desatentas ou agressivas, “chutam” uma resposta qualquer, ou se desinteressam da atividade).
• Na medida do possível, as instruções devem ser na forma de perguntas ou suscitar a reflexão. Ao invés de simplesmente dar informações às crianças, os pais e professores devem dar às crianças a oportunidade de refletir sobre um problema ou uma tarefa, fazer suposições (hipóteses fundamentadas), imaginar sua própria estratégia ou deduzir sua própria resposta. 

Os elementos acima estão ilustrados nos casos de Alice²¹ e de Lukas.²²

• O caso de Alice. Há vários meses, essa menina de dois anos e meio era capaz de reconhecer um, dois ou três objetos. E seus pais desejavam ampliar seus conhecimentos até o número quatro, logo além de suas competências. No lugar de simplesmente denominar conjuntos de quatro objetos para ela, eles lhe perguntaram sobre conjuntos de quatro objetos. Alice respondia muitas vezes decompondo os conjuntos que não reconhecia em dois conjuntos familiares com dois objetos cada. Seus pais aproveitavam então sua resposta dizendo-lhe: “Dois mais dois é igual a quatro.” Aos 30 meses de idade, quando lhe mostram uma foto com quatro cachorrinhos, Alice coloca dois dedos da sua mão esquerda em dois cachorrinhos e diz: “Dois”. Mantendo essa posição, ela coloca dois dedos da mão direita nos dois outros cachorrinhos e diz: “Dois”. Depois, ela utiliza a relação conhecida “2 mais 2 é igual a 4” (que seus pais lhe ensinaram) para especificar a cardinalidade do conjunto.
• O caso de Lucas. No âmbito de um jogo matemático no computador, a operação 6+6 foi apresentada ao Lucas. Ela acertou a soma contando. Logo depois, lhe foi a perguntado 7+7. Ele sorriu e respondeu rapidamente “Treze”. Quando o computador lhe indicou que a soma era 14, ele pareceu perplexo. Algumas perguntas depois, lhe foi perguntado 8+8, e ele comentou: “Eu ia dizer 15, porque 7+7 era igual a 14. Mas antes, 6+6 era igual a 12, e eu tinha certeza que 7+7 era igual a 13, mas era 14. Então, vou responder que 8+8 é igual a 16.”

Futuras orientações

Ainda há muitas coisas a aprender sobre o desenvolvimento da matemática em crianças em idade pré-escolar. Será que a habilidade do reconhecimento verbal dos números aos dois anos permite predizer que ela estará pronta para a pré-escola ou será bem-sucedida em matemática? Caso seja, será que uma intervenção focada em exemplos e contraexemplos vai permitir que as crianças em risco de insucesso escolar alcancem seus pares? Quais outros conceitos ou habilidades na idade de dois ou três anos podem indicar que a criança está pronta para a pré-escola ou que será bem-sucedida em matemática na escola? Qual é a eficácia dos programas de matemática para a primeira infância que estão sendo desenvolvidos atualmente?

Conclusões

Ao contrário das convicções de muitos educadores para a primeira infância, o ensino da matemática para crianças de apenas dois anos de idade faz sentido.^23,24,25,26 Como mostra claramente a figura 1, esse ensino deve começar ajudando as crianças a desenvolver um conceito cardinal dos números intuitivos, e a habilidade de reconhecer e denominar conjuntos de um a três objetos com o nome correto do número. A figura 1 mostra também que esses aspectos do conhecimento dos números constituem elementos-chave para as operações numéricas posteriores e, muitas vezes, faltam em crianças com deficiências em matemática.²⁷ O ensino precoce não significa impor conhecimentos às crianças em idade pré-escolar, treinando-as com cartões pedagógicos, ou fazendo-as decorar operações aritméticas. O estímulo à percepção dos números e ao domínio das operações deveria estar focado em ajudar as crianças a descobrirem os padrões e as relações e em estimulá-las a inventar suas próprias estratégias de raciocínio.

Referências

1. Baroody AJ, Dowker A. The development of arithmetic concepts and skills:  Constructing adaptive expertise. In: Schoenfeld A, ed. Studies in mathematics thinking and learning series.  Mahwah, NJ: Lawrence Erlbaum Associates; 2003.
2. Kilpatrick J, Swafford J, Findell B, eds. Adding it up: Helping children learn mathematics. Washington, DC: National Academy Press; 2001.
3. Baroody AJ, Lai ML, Mix KS. The development of number and operation sense in early childhood. In: Saracho O, Spodek B, eds. Handbook of research on the education of young children. Mahwah, NJ: Erlbaum; 2006: 187-221.
4. Clements D, Sarama J, DiBiase AM, eds. Engaging young children in mathematics: Standards for early childhood mathematics education. Mahwah, NJ: Lawrence Erlbaum Associates; 2004: 149-172.
5. Ginsburg HP, Klein A, Starkey P. The development of children’s mathematical knowledge: Connecting research with practice. In: Sigel IE, Renninger KA, eds.  Child psychology in practice. 5th Ed. New York, NY: Wiley & Sons; 1998; 401–476. Handbook of child psychology, vol 4.
6. Baroody AJ. Why children have difficulties mastering the basic number facts and how to help them. Teaching Children Mathematics 2006;13:22–31.
7. Baroody AJ, Thompson B, Eiland M. Fostering the fact fluency of grade 1 at-risk children. Paper presented at: The annual meeting of the American Educational Research Association. April, 2008. New York, NY.
8. Gersten R, Chard, D. Number sense: Rethinking arithmetic instruction for students with mathematical disabilities. The Journal of Special Education 1999;33(1):18–28.
9. Jordan NC. The need for number sense. Educational Leadership 2007;65(2):63–66.
10. Dowker AD. Individual differences in arithmetic: Implications for psychology, neuroscience and education. Hove, England: Psychology Press; 2005.
11. Baroody AJ. The development of kindergartners' mental-addition strategies. Learning and Individual Differences 1992;4:215-235.
12. Baroody AJ, Eiland M, Thompson B. Fostering at-risk preschoolers' number sense. Early Education and Development 2009;20:80-120.
13. Mix KS, Sandhofer CM, Baroody AJ. Number words and number concepts: The interplay of verbal and nonverbal processes in early quantitative development. In: Kail R, ed. Advances in child development and behavior, vol 33. New York, NY: Academic Press; 2005: 305-346.
14. Baroody AJ, Li X, Lai ML. Toddlers’ spontaneous attention to number. Mathematics Thinking and Learning 2008;10:1-31.
15. Dehaene S. The number sense. New York, NY: Oxford University Press; 1997.
16. Wynn K. Numerical competence in infants. In; Donlan C, ed. Development of mathematical skills. Hove, England: Psychology Press; 1998: 1-25.
17. Benoit L, Lehalle H, Jouen F. Do young children acquire number words through subitizing or counting? Cognitive Development 2004;19:291–307.
18. Baroody AJ, Lai ML, Li X, Baroody AE. Preschoolers’ understanding of subtraction-related principles. Mathematics Thinking and Learning 2009;11:41–60.
19. Mazzocco M, Thompson R. Kindergarten predictors of math learning disability. Learning Disabilities Research & Practice 2005;20:142-155.
20. Baroody AJ, Coslick RT. Fostering children's mathematical power: An investigative approach to K-8 mathematics instruction. Mahwah, NJ: Erlbaum; 1998.
21. Baroody AJ, Rosu L. Adaptive expertise with basic addition and subtraction combinations: The number sense view. In: Baroody AJ, Torbeyns T. chairs. Developing Adaptive Expertise in Elementary School Arithmetic. Symposium conducted at: The annual meeting of the American Educational Research Association. April, 2006. San Francisco, CA.
22. Baroody AJ. Fostering early number sense. Keynote address at: The Banff International Conference on Behavioural Science. March, 2008. Banff, Alberta.
23. Baroody AJ, Li X. Mathematics instruction that makes sense for 2 to 5 year olds. In: Essa EA, Burnham MM, eds. Development and education: Research reviews from young children. New York: The National Association for the Education of Young Children; 2009: 119-135.
24. Bredekamp S, Copple C. Developmentally appropriate practice in early childhood programs.  Washington, DC:  National Association for the Education of Young Children; 1997.
25. Copley J, ed.  Mathematics in the early years, birth to five. Reston, VA: National Council of Teachers of Mathematics; 1999.
26. Copley J, ed. The young child and mathematics. Washington, DC: National Association for the Education of Young Children; 2000.
27. Landerl K, Bevan A, Butterworth B. Developmental dyscalculia and basic numerical capacities: A study of 8-9 year old students. Cognition 2004;93:99–125.